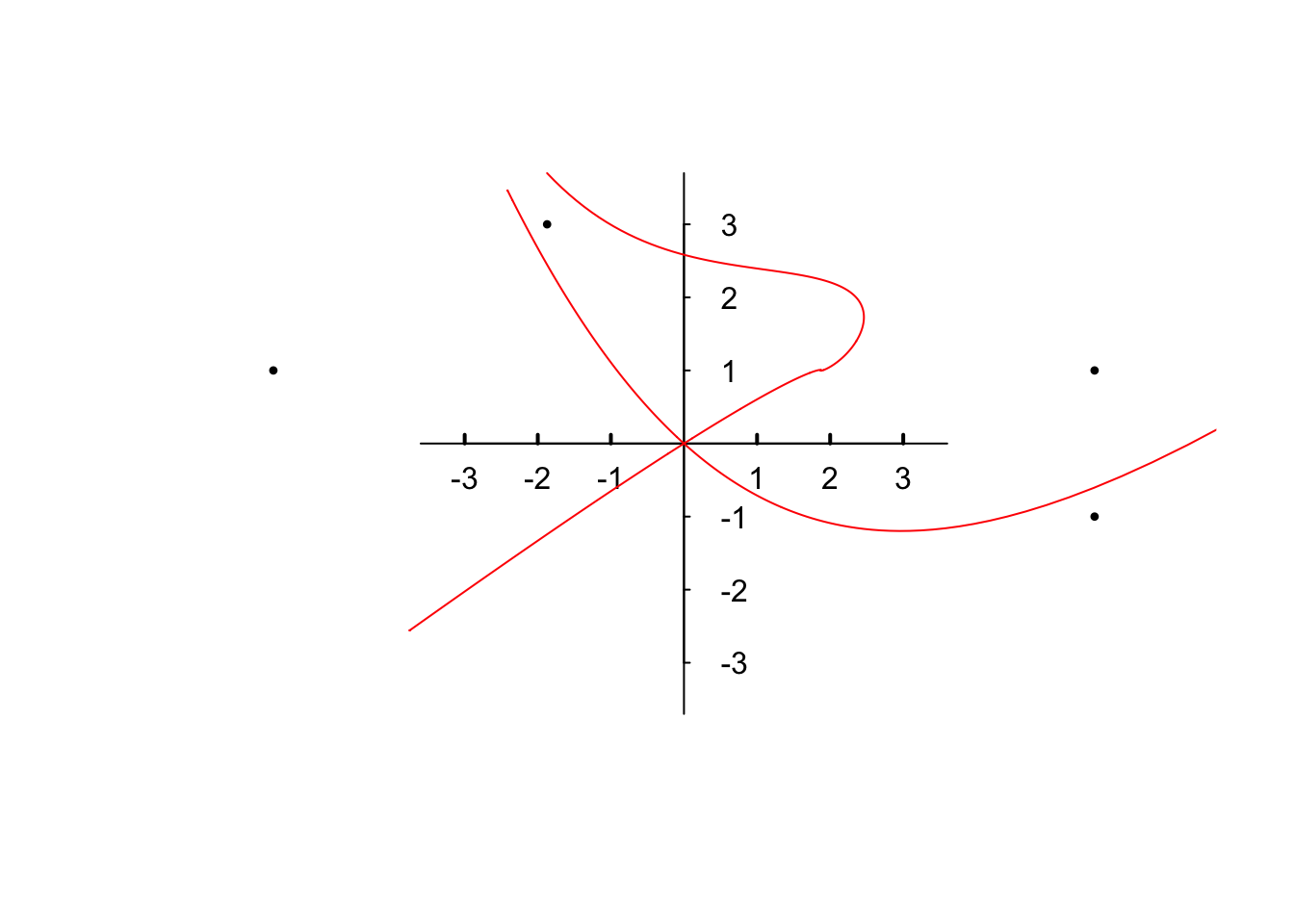7.3 The DeSolve Package for Differential Equations

library(deSolve)
source('~/Dropbox/Project-R/MyToolbox/combineMAT.r') # combine matrices w diff size
source('~/Dropbox/Project-R/MyToolbox/DrawAxes.r') # Draw axes in the center 
EQNS <- function(t, status, parms){
  with(as.list(status),{
    dX <- 2*Y-2*X^2
    dY <- 4*X-Y-3*X^2
    list(c(dX,dY))
  })
}

dt <- 0.01; ## Step size in t
n <- 5 ## Number of initial value sets

# Each row is one initial value set in the form of
# X0, Y0, t_min, t_max, delta_t
# If t_min < t_max, solve ode backwards
ivp <- matrix(c(0.001, -0.0001, 0, 5, dt,
                -0.001, -0.001, 3, 0, -dt,
                -0.001, -0.001, 0, 2.8, dt,
                0.001, -0.001, 2.37, 0, -dt,
                -1, 3.7, 0, 5, dt),
              nrow = n, byrow = TRUE)

# Numeric solution
userdata <- matrix(NA) 
for (i in 1:n){
  status <- c(X = ivp[i,1],Y = ivp[i,2])
  t <- seq(ivp[i,3],ivp[i,4],ivp[i,5])
  out <- ode(y = status, times = t, func = EQNS, parms = NULL)
  
  # "out" has three columns: t, x, y
  # Using out[, -1] excludes the first column, which is t.
  # First column of userdata are sequential numbers 1, 2, 3, ...
  # Rest odd columns of userdata is y
  # Even columns of userdata is x
  # Did not use cbind because all the 'out' from ode are different in row dimension
  # Did not use rbind for the convenience of graphing
  userdata <- combineMAT(userdata,out[,-1])
}

# Setting the range
# Find the max of the absolute value of x and y separately
# The factor 0.7 is from trial-and-error to make the plot look nice
xabs <- 0.7 * max(abs(userdata[,seq(2,2*n,2)])) 
yabs <- max(abs(userdata[,seq(3,2*n+1,2)])) 

# Blank plot with axes labels
DrawAxes(-xabs, xabs, -yabs, yabs, 'x','y', 0)
axis(1,at = c(-3,-2,-1,1,2,3),hadj = 0.5, padj = -1,
      lwd.ticks = 2, tick = TRUE, tck = 0.015, pos = 0)
axis(4, at=c(-3,-2,-1,1,2,3), padj = 0.5,
      tick = TRUE, labels = TRUE, las = 2, tck = -0.01, pos = 0)

# Draw solution curves
for (i in 1:n){
  par(new=TRUE) # Add to existing plot
  plot(userdata[,2*i], userdata[,2*i+1], type = 'l', col='red',
     xlim = c(-xabs, xabs), ylim = c(-yabs, yabs),
     xlab = '', ylab = '',axes = FALSE)
}

# Draw points of random initial conditions
par(new=TRUE) # Add to existing plot
plot(c(3, 3, -1, -3), c(1, -1, 3, 1), type = 'p', pch=20, cex=0.7, 
     xlim = c(-xabs,xabs), ylim = c(-yabs,yabs),
     xlab = '', ylab = '',axes = FALSE)